¶ 서문: 수학의 재발명과 시스템 아키텍처
현대 인공지능(AI) 기술의 비약적인 발전은 단순히 알고리즘의 개선이나 컴퓨팅 파워의 증대에만 기인하지 않는다. 그 기저에는 현실 세계의 복잡성을 기계가 이해할 수 있는 언어로 변환하는 거대한 지적 체계, 바로 수학이 존재한다. 본 보고서는 업로드된 문서 '00 AI 초등수학 가이드북' 을 핵심 텍스트로 삼아, 이 가이드북이 제시하는 새로운 수학적 패러다임인 "시스템 아키텍처로서의 수학"을 심층적으로 분석한다. 저자의 선언문에서 밝히고 있듯이, 이 문서는 수학을 단순한 계산 기술(Calculation Skill)의 집합으로 보지 않고, 지능형 시스템을 설계하는 구조적 언어이자 엔지니어링 의사결정의 도구로 재정의한다.
우리는 특히 책의 첫 번째 섹션인 'Section 1. 데이터의 기초: 추상화의 탄생'의 개요를 확립하고, 그 시작점인 'Chapter 1. 수(Number)/압축(Compression)'을 가이드북 고유의 서사 구조(Basecamp, Architect's Challenge, Math Debugging, Schema)에 따라 정밀하게 해부할 것이다. 이 과정에서 본 보고서는 원문의 내용을 충실히 반영함과 동시에, 인지과학, 정보이론, 최신 딥러닝 프레임워크(PyTorch), 그리고 시스템 엔지니어링의 트레이드오프 이론 등 방대한 외부 연구 자료를 통합하여, 단순한 요약을 넘어선 전문가 수준의 통찰을 제공하는 것을 목표로 한다.1
¶ Section 1 개요: 데이터의 기초와 추상화의 기원
¶ 1.1 섹션의 구조적 의의: 현실에서 데이터로
Section 1. 데이터의 기초: 추상화의 탄생은 전체 가이드북의 주춧돌(Cornerstone) 역할을 수행한다. AI 시스템이 현실 세계를 인지하고 처리하기 위해서는, 무한하고 연속적이며 잡음(Noise)으로 가득 찬 아날로그 현실을 유한하고 이산적인 디지털 데이터로 변환하는 과정이 선행되어야 한다. 이 변환의 과정이 바로 **추상화(Abstraction)**이며, Section 1은 이 추상화를 가능하게 하는 가장 원자적인 도구인 **수(Number), 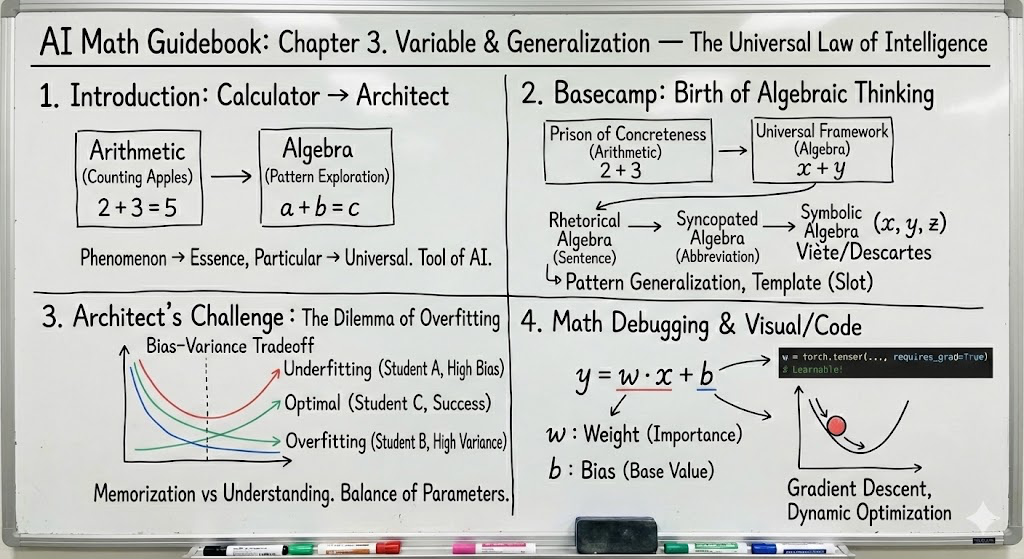0(Zero), 변수(Variable)**를 탐구한다.
이 섹션은 단순히 초등 수학의 산술 연산을 복습하는 단계가 아니다. 성인 독자, 특히 엔지니어와 시스템 아키텍트들에게 우리가 무의식적으로 사용하는 이 기초 개념들이 사실은 인류가 고안한 고도의 **"정보 압축 알고리즘"**이자 **"시스템 확장성을 위한 프로토콜"**임을 일깨우는 데 그 목적이 있다. 본 섹션에서 확립된 '데이터를 수치적 추상화로 바라보는 관점'은 이후 이어질 공간(Space), 최적화(Optimization), 불확실성(Uncertainty) 섹션들을 지탱하는 논리적 기반토양(Foundation)이 된다.
¶ 1.2 핵심 주제 및 시스템적 가치 분석
이 섹션은 다음 세 가지 챕터로 구성되어 있으며, 각 개념은 현대 AI 아키텍처의 특정 기능과 밀접하게 연관된다. 이를 시스템적 관점에서 분석하면 다음과 같다.
¶ Chapter 1. 수(Number)와 압축(Compression)
- 개념적 정의: 수는 개별적이고 구체적인 사물의 감각적 맥락(Context)—색상, 질감, 맛 등—을 제거하고, 오직 '양(Quantity)'이라는 정보만을 남기는 최초의 **데이터 압축 기술(Data Compression Technology)**이다. 정보이론 관점에서 이는 원본 데이터의 엔트로피를 급격히 낮추어 처리 효율을 극대화하는 과정이다.
- 시스템적 가치: 이는 현대 AI 및 데이터 사이언스에서 스칼라(Scalar) 데이터 타입의 기원이 된다. 현실의 물리적 현상이 0과 1의 조합인 수치 데이터로 변환되어 저장, 전송, 연산될 수 있는 근거를 제공한다. 즉, 수는 아날로그 현실을 디지털 컴퓨팅 환경으로 매핑(Mapping)하는 첫 번째 인터페이스다.1
¶ Chapter 2. 0(Zero)과 시스템(System)
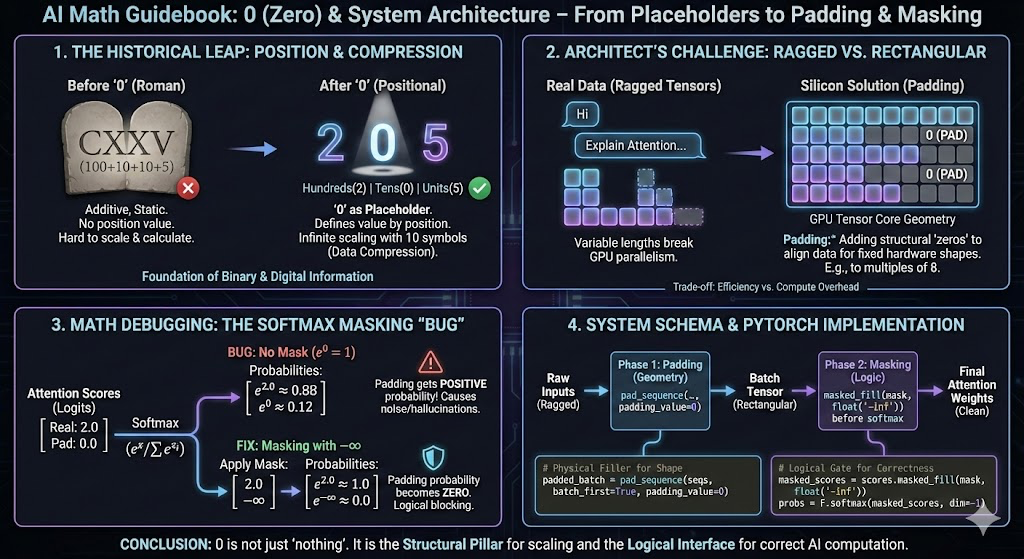
- 개념적 정의: 0은 '없음(Nothingness)'을 나타내는 수일 뿐만 아니라, 위치값 기수법(Positional Notation)을 완성하는 **구조적 공백(Structural Void)**이다. 빈 자리를 0으로 마킹(Marking)함으로써 우리는 자릿수를 유지하고, 유한한 심볼로 무한한 크기의 수를 표현할 수 있게 되었다.
- 시스템적 가치: 이는 AI 시스템의 **스케일링(Scaling)**과 **차원 유지(Dimensionality Preservation)**의 핵심이다. 현대 딥러닝의 희소 행렬(Sparse Matrix) 연산이나 드롭아웃(Dropout) 기법, 패딩(Padding) 등에서 0은 연산 효율을 높이거나 데이터의 구조적 정합성을 맞추는 버팀목 역할을 한다. 0이 없다면 위치 정보가 소실되어 고차원 텐서 연산 자체가 불가능하다.
¶ Chapter 3. 변수(Variable)와 일반화(Generalization)
- 개념적 정의: 구체적인 수치 대신 문자(x, y)를 사용하여 관계의 패턴을 서술하는 대수적(Algebraic) 기술이다. 이는 개별 사실(Instance)에 갇히지 않고 보편적인 법칙(Rule)으로 사고를 확장하는 도구다.
- 시스템적 가치: AI 모델의 핵심인 **파라미터(Parameter)**와 **가중치(Weight)**가 바로 변수다. 라는 식에서 와 는 고정된 값이 아니라 데이터를 통해 학습되는 가변적인 값이며, 이를 통해 모델은 학습 데이터 이외의 새로운 상황(Unseen Data)에 대응하는 **일반화 능력(Generalization Capability)**을 획득한다. 변수는 AI 시스템이 '기억'을 넘어 '추론'으로 나아가는 DNA다.1
¶ 1.3 섹션 간의 유기적 연결성
Section 1의 통찰은 고립되어 있지 않고 전체 가이드북의 서사를 관통한다.
- Section 2(공간)로의 연결: Section 1에서 압축된 수치(스칼라)들은 Section 2에서 여러 개가 묶여 **벡터(Vector)**와 **행렬(Matrix)**로 확장된다. 수 하나하나는 점이 되고, 수들의 관계는 공간상의 거리와 방향으로 재해석된다.
- Section 3(최적화)로의 연결: 변수(Variable) 개념은 최적화의 대상이 된다. '학습'이란 결국 오차 함수(Error Function)라는 지형 위에서 가장 적절한 변수 값을 찾아내는 탐험 과정임을 이해하게 된다.
- Section 9(에이전트)로의 연결: 궁극적으로 이 기초적인 추상화 도구들이 모여, 스스로 계획하고 행동하는 지능형 에이전트 시스템을 구축하는 기반이 된다.
결론적으로 Section 1은 **"어떻게 기계에게 세상을 가르칠 것인가?"**라는 질문에 대해, **"먼저 세상을 수라는 언어로 번역(Encoding)해야 한다"**는 답을 제시하는 과정이다.